Actually we can say that Normal distribution is the most widely known and used of all distributions. Because the normal distribution approximates many natural phenomena so well, it has developed into a standard of reference for many probability problems So Normal distribution characteristics is :
• Symmetric & bell shaped
• Continuous for all values of X between -∞ and ∞ so that each conceivable interval of real numbers has a probability other than zero.
• -∞ ≤ X ≤ ∞
• Two parameters, μ and σ. Note that the normal distribution is actually a family of distributions, since μ and σ determine the shape of the distribution.
• The rule for a normal density function is e21 = )
![f(x) = EXP[-(x-mu)**2/(2*sigma**2)]/(sigma*SQRT(2*PI))](http://www.itl.nist.gov/div898/handbook/eda/section3/eqns/norpdfg.gif)
where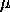 
is the location parameters and 
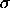is the scale parameters. The case where 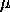= 0 and 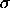= 1 is called the standard normal distribution. The equation for the standard normal distribution is
![f(x) = EXP[-x**2/2]/SQRT(2*PI)](http://www.itl.nist.gov/div898/handbook/eda/section3/eqns/norpdf.gif)
• The notation N(μ, σ2) means normally distributed with mean μ and variance σ2. If we say X ∼ N(μ, σ2) we mean that X is distributed N(μ, σ2).
• About 2/3 of all cases fall within one standard deviation of the mean, that is
P(μ - σ ≤ X ≤ μ + σ) = .6826.
• About 95% of cases lie within 2 standard deviations of the mean, that is
P(μ - 2σ ≤ X ≤ μ + 2σ) = .9544
